Comment calculer le THD et le PF？

Comment calculer le THD et le PF？

 

Analyse de la distorsion harmonique totale (THD) et évaluation du facteur de puissance Dans cette discussion, nous explorerons les méthodologies permettant d'évaluer la distorsion harmonique totale ainsi que les calculs du facteur de puissance.

La distorsion harmonique totale (THD) est une mesure reflétant la fusion de fréquences harmoniques juxtaposées à la fréquence primaire, telle que 60 Hz, sur un circuit. Il englobe toutes les fréquences harmoniques présentes. Le THD peut être associé à des harmoniques de courant ou de tension. Pour quantifier la distorsion de la tension de ligne, appliquez la formule suivante :

 

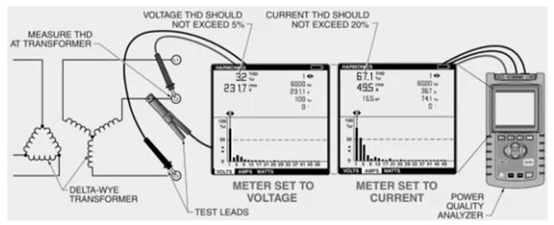
Figure 1. La mesure du THD doit être effectuée au niveau du transformateur, et non à côté de la charge.

Où Vn_rms est la tension efficace de la nième harmonique et Vfund_rms désigne la tension efficace de la fréquence fondamentale. Une onde sinusoïdale pure, dépourvue d'harmoniques supérieures, comme une source de tension impeccable, présente un THD de 0 %. Toute valeur THD supérieure à zéro indique une distorsion de l'onde sinusoïdale. Les chiffres du THD sont généralement présentés sous forme de pourcentages, par exemple 5 % ou 50 %. Le THD peut être évalué pour les signaux de courant et de tension.

Les courants harmoniques proviennent de charges non linéaires qui consomment du courant par impulsions. Les harmoniques de tension proviennent de ces courants traversant diverses résistances du système. Le courant du transformateur induit une chute de tension aux bornes de ses bobines. Lorsque le courant est pulsé, la tension reflète cette pulsation. Une distorsion de tension excessive est préjudiciable car elle sert de conduit aux harmoniques vers des charges linéaires, telles que les moteurs électriques. Les harmoniques de tension introduisent un échauffement supplémentaire dans les systèmes de distribution d’énergie et les appareils connectés.

 

Mesure du THD

Dans les circuits de dépannage pour les harmoniques, veillez à mesurer à la fois le THD de tension et le THD de courant. Les résultats idéaux garantissent que le THD de tension ne dépasse pas 5 % et que le THD actuel reste inférieur à 20 % de la fréquence de base. Le THD doit être évalué au niveau du transformateur pour un calcul précis du THD à l'échelle du système (comme illustré dans l'illustration 1). Les lectures THD côté charge offrent les valeurs les plus élevées puisque l'annulation des harmoniques ne s'est pas produite dans l'ensemble du système.

 

Lors de la mesure du courant THD dans des conditions de pleine charge, le THD s'apparente à la distorsion totale de la demande (TDD). TDD est le quotient des harmoniques de courant par rapport au courant de charge ultime. Une mesure THD est exécutée lors du diagnostic ou du test des systèmes. Le TDD s'écarte du THD car le TDD est comparé à la mesure du courant de crête au fil du temps. Le THD mesure uniquement le courant au moment de la mesure. Le rôle du TDD est de prendre en compte les cas où le THD est élevé, alors que la charge globale est relativement faible. Dans de telles circonstances, le TDD est modeste, minimisant la surchauffe.

 

Facteur de puissance

 

Power factor delineates the ratio of authentic power to apparent power in a circuit or distribution network. Every AC circuit is comprised of real, reactive, harmonic, and apparent (aggregate) power. True power, in watts or kilowatts, is expended by motors, lighting, and other apparatuses to execute functional tasks. Reactive power, in volt-amperes reactive or kilovolt-amperes reactive, is stored and discharged by inductors and capacitors. Reactive power materializes as phase displacement between current and voltage waveforms. Harmonic power, in volt-amperes or kilovolt-amperes, is dissipated due to harmonic distortion. Apparent power, in volt-amperes or kilovolt-amperes, is the vectorial sum of true power, reactive power, and harmonic power. Apparent power isn't a simple accumulation but a vector summation.

 

Displacement Power Factor

 

The displacement power factor is the ratio of genuine power to apparent power attributable to phase displacement between current and voltage (as shown in Illustration 2). Capacitors can frequently be integrated into a circuit or distribution network to rectify the displacement power factor. Its computation is as follows:

PF = cos(θ)

where PF signifies displacement power factor and θ is the discrepancy between voltage and current phases in degrees. Note: DPF or PFD may occasionally substitute PF to denote displacement power factor.

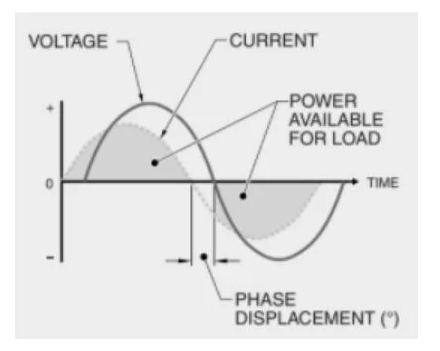
Figure 2. Displacement power factor enables calculation of the power genuinely accessible for a load.

 

 

The presence of harmonics introduces complexity into the discussion of power factor. The distortion power factor, defined as the ratio of true power to apparent power due to Total Harmonic Distortion (THD), cannot be mitigated simply by adding capacitors to a circuit. This is because the impedance of capacitors decreases with an increase in frequency, potentially turning them into sinks for high-frequency harmonics rather than effective compensators.

 

To address the distortion power factor, specialized solutions are employed. These include special types of transformers designed to handle harmonic loads or tuned harmonic filters that consist of a combination of capacitors and inductors. Such filters are specifically engineered to resonate at harmonic frequencies, effectively absorbing or cancelling out these distortions.

 

The calculation of the distortion power factor involves assessing the impact of harmonic content on the overall power factor, reflecting the diminished efficiency caused by the presence of these higher-order frequencies in the electrical system.

The distortion power factor is calculated as follows:

.

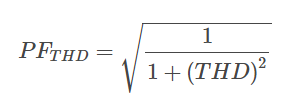
where
PFTHD = distortion power factor
THD = total harmonic distortion

The total power factor is the product of the displacement power factor and the distortion power factor and is calculated as follows:

PFTot = PF × PFTHD

where
PFTot = total power factor
PF = displacement power factor
PFTHD = distortion power factor

For example, what is the total power factor when the displacement between voltage and current is 25°, and the THD is 49% (0.49)? The displacement power factor is calculated as follows:

PF = cos(θ)
PF = cos (25°)
PF = 0.906

The distortion power factor is calculated as follows:

.

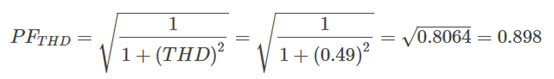The total power factor is calculated as follows:

PFTot = PF × PFTHD
PFTot = 0.906 × 0.898
PFTot = 0.814

Understanding the total power factor is crucial as it directly correlates with apparent power, which is fundamental in sizing components within a power distribution system. Apparent power serves as a key metric for ensuring that all elements in the system are appropriately rated to handle the electrical load without being overloaded.

 

Current Crest Factor

 

The current crest factor, defined as the ratio of the waveform's peak value to its RMS value, serves to indicate the extent of distortion in the waveform. Its calculation provides insights into the waveform's quality, with higher factors pointing to greater levels of distortion. The formula for determining the current crest factor is as follows:

.

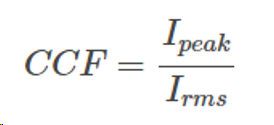where
CCF = current crest factor
Ipeak = peak value (in A)
Irms = root mean square value (in A)

For example, what is the current crest value of a perfect sine waveform? In a perfect sine waveform with a peak value of 1, the rms value is 0.707.

.

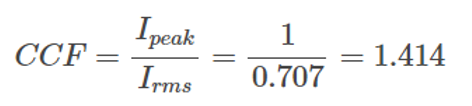An elevated current crest factor can result in excessive heat generation within circuits and devices. For instance, on a 120V circuit powering digital equipment such as computers, a distorted current waveform might display a crest factor ranging from 2 to 6 (consult Figure 3). Typically, circuits with a higher current crest factor contain a greater proportion of energy in their higher harmonics.

 

A power source is obligated to provide the peak power needed by the circuit, matching the specified voltage and current demands. A conventional backup power system, such as an uninterruptible power supply for computers, is capable of delivering a current crest factor of 3 when operating at full capacity but may experience augmented crest factors under lighter load conditions.

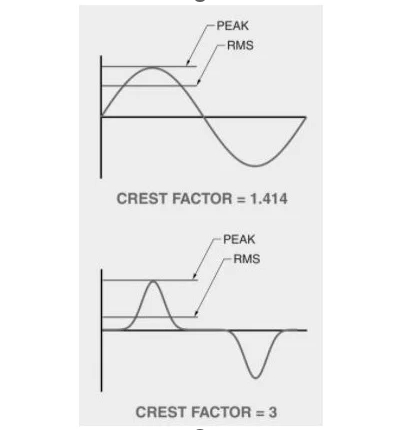
Figure 3. The current crest factor comparison

 

 Source Impedance

 

L'impédance de la source a un impact sur le facteur de crête généré par les charges non linéaires. Lorsqu'un seuil de tension spécifique est atteint, l'alimentation lance la charge d'un condensateur de lissage. Lorsque l'impédance de la source est minimale, la pointe de courant dans le condensateur est importante, ce qui entraîne une brève durée de charge. À l’inverse, une impédance plus élevée limite le flux de courant, prolongeant ainsi la période de charge du condensateur. Cet intervalle de charge prolongé diminue efficacement le facteur de crête. On peut augmenter l'impédance de la source grâce à l'incorporation de selfs de ligne ou de transformateurs d'isolement de commande.